Staying arbitrage-free with Andreasen-Huge one-step interpolation
Not long ago, I wrote about Andreasen-Huge arbitrage-free volatility interpolation method. What we get out of Andreasen-Huge method, is a list of discrete option prices. What about option prices for strikes not on the grid?
March 8, 2018
Not long ago, I wrote a post about Andreasen-Huge arbitrage-free volatility interpolation method, showing that using a spline for the one-step local volatility instead of a piecewise-constant (or better, a piecewise-linear) function was not necessarily a great idea.
What we get out of Andreasen-Huge method, is a list of discrete option prices. What about option prices for strikes not on the grid?
In this case we still need some kind of interpolation. If we work directly with option prices, as described in their paper, the simplest seems to try a cubic spline on those option prices. In reality, a C2 cubic spline is likely to introduce arbitrages as it does not preserve convexity. How bad is it?
It can be really bad. Below is an example based on the market mid prices of 1m SPX options as of February 5, 2018. It is an example where calibration is not perfect (likely because there is a small arbitrage in the quotes, within the bid-ask spread).
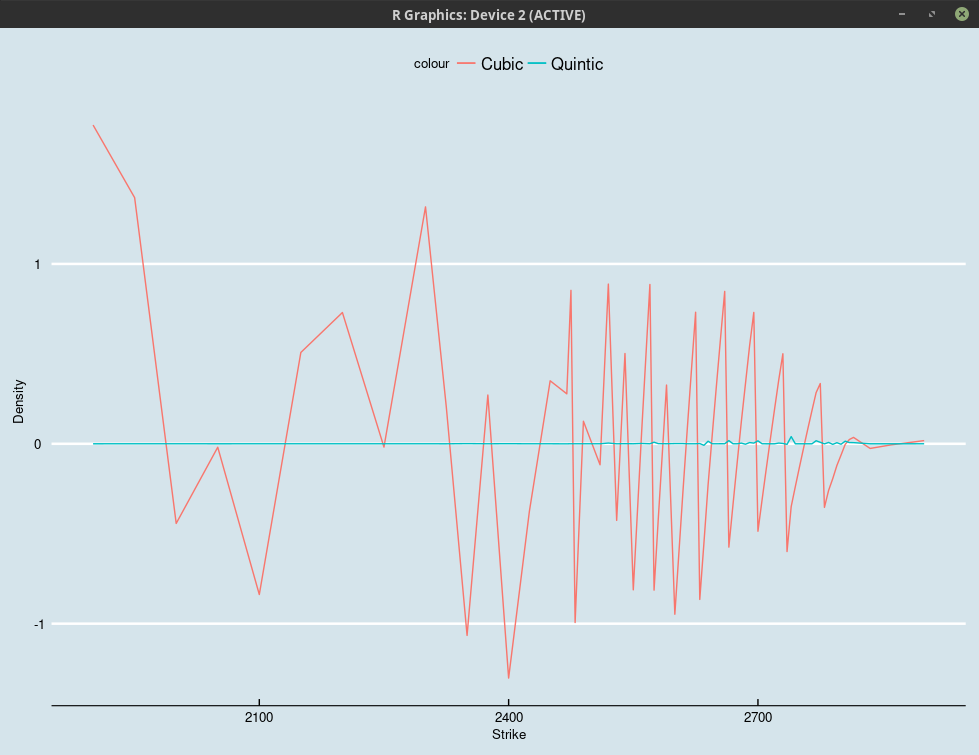
Probability density obtained using a C2 Cubic vs a C2 Quintic interpolation on Andreasen-Huge prices.
Indeed, a C2 cubic spline is not going to respect the second derivative values at the interpolating nodes. A C2 quintic Hermite spline can do so. In the above plot, we estimate the first and second derivatives by a parabola on three nodes. While it looks better, it can still lead to negative density in between nodes, as, again, it is not convexity preserving. Interestingly, while there exists some algorithms to attempt to preserve convexity, such as the one of Hyman, it can be proved that polynomial splines can not preserve convexity in the general case (the link is on a paper on quadratic splines, but the general result is mentioned, I could not find a link to the original result “On the existence of shape preserving interpolation operators”).
A better solution is to compute the density via the Fokker-Planck one-step implicit Euler method, and integrate it to obtain vanilla options prices at, or in between nodes as shown in my book, similarly to what is done in the arbitrage-free SABR method of Hagan et al.. In this case, by construction, we can guarantee the arbitrage-free property.
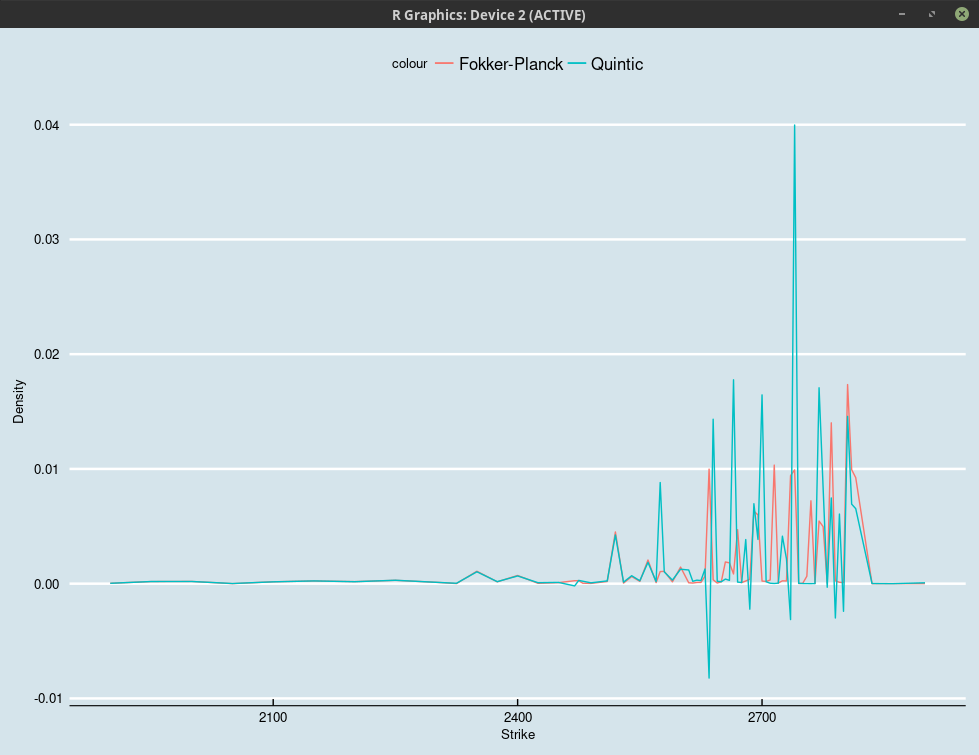
Probability density obtained using a C2 Quintic interpolation on Andreasen-Huge prices vs. the integration of the Fokker-Planck one-step density.
There are still a lot of spikes (positive), would a piecewise-linear discrete local volatility be better?
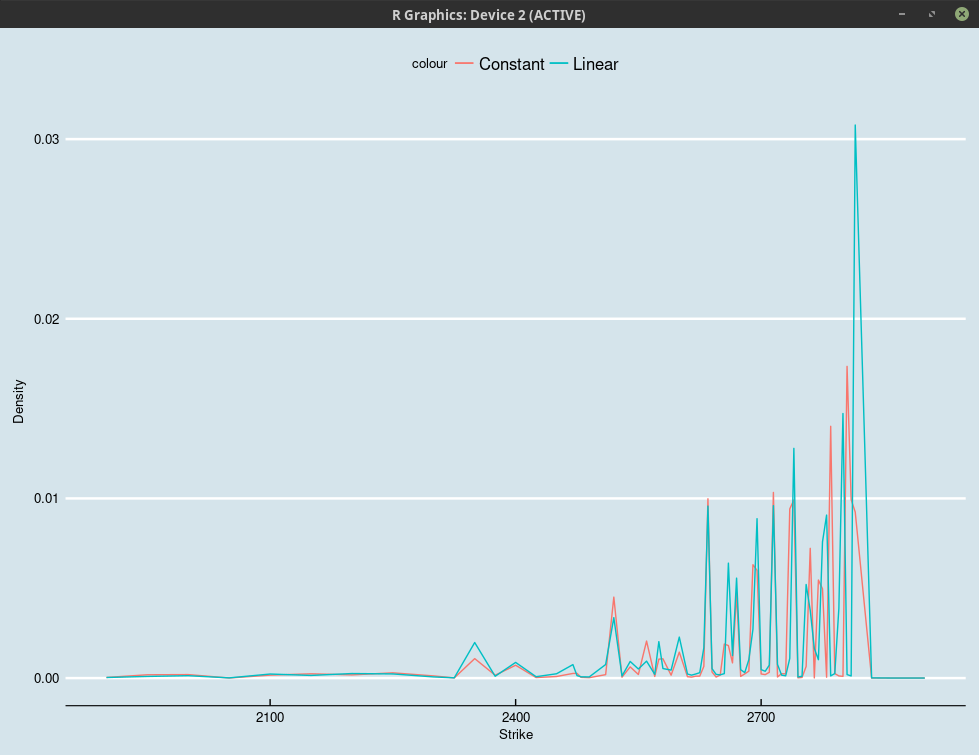
Probability density obtained by numerically differentiating the integration of the Fokker-Planck one-step density.
The answer is no. The Andreasen-Huge method has in general the tendency of producing such very spiky density. If we consider a nicer set of market quotes (from January 23, 2018), here is how the Fokker-Planck density looks like:
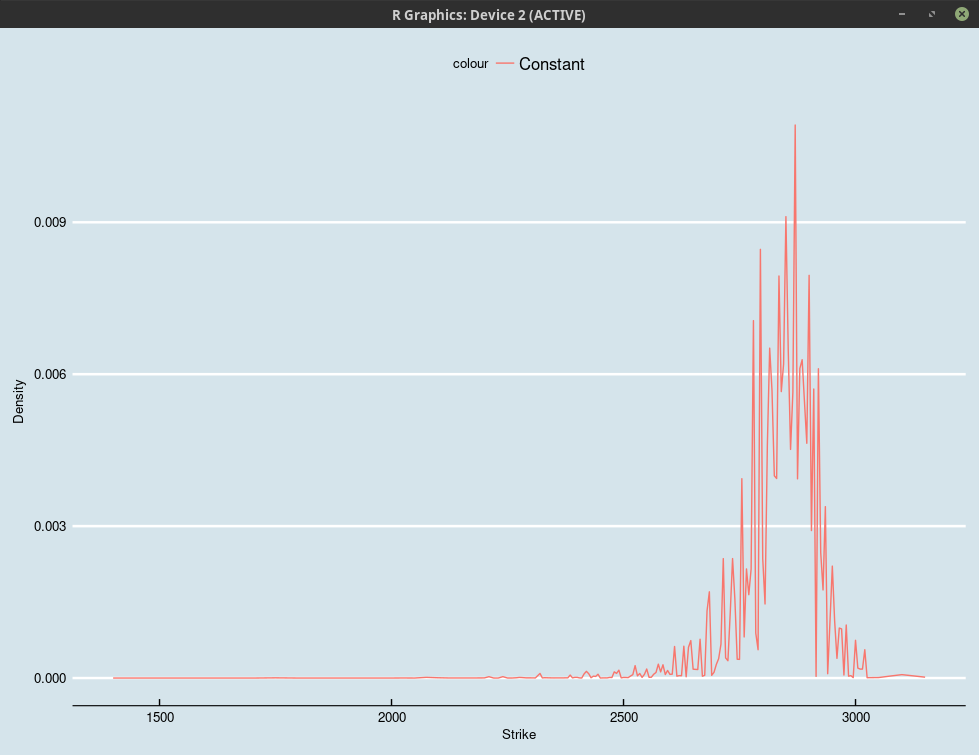
Fokker-Planck one-step density.
One way to mitigate this would be to use (much) less local volatility constants than the number of market strikes.