Klein summation and Monte-Carlo simulations
In parallelized Monte-Carlo simulations, the order of summation is not always the same. When the mean is calculated in running fashion, this may create an artificial randomness in results which ought to be reproducible. Does the Klein summation help addressing this issue? Are there better alternatives?
August 28, 2022
The straightforward and naive ways of calculating the mean and variance of the samples of a Monte-Carlo simulation may introduce artificial errors in the results. Monte-Carlo simulations are inherently parallelisable. It is possible and often desirable to run such a parallel simulation using a consistent set of random numbers, such that the results of the simulation are reproducible. However, the operating system scheduling of the simulation on the multiple cores or CPUs implies some randomness in the order of the completed batches of results, due to the varying load of the CPUs. When the mean and variance of the Monte-Carlo simulation are calculated in running manner, the results obtained may differ due to the order of the terms in the summations involved, because of limits of accuracy imposed by the IEEE 64-bit floating-point standard. The differences may appear minor, but are amplified in finite-difference based sensitivities based on the mean, reusing the same random numbers (which is a standard practice).
On one hand, the problem of calculating accurately the mean and variance has been studied in details, some recommended readings are Chan Golub and Leveque (1983) Algorithms for computing the sample variance: Analysis and recommendations, Chan and Lewis (1979) Computing standard deviations: accuracy.
On the other hand, Kahan (1965) Pracniques: further remarks on reducing truncation errors, Klein (2006) A generalized kahan-babuška-summation-algorithm propose to add some correction terms for the problem of calculating a running sum with increased accuracy.
Klein suggests a second order correction, and shows it to be more accurate than the more widely known Kahan summation on a example summing 50 million 32-bit floating point numbers uniformly distributed in the interval (0,1). This looked like a good candidate to try out on my problem. And indeed, this solves some visible issues we may see calculating mean, variance and Monte-Carlo greeks in 64-bit floating point arithmetic. But the simpler Kahan summation also solved the issues.
Then I wondered if I could find a use case where Klein would prove more appropriate. As a first step, I tried to reproduce the results presented in Klein’s 2006 paper. Somewhat surprisingly, I did not reproduce the results:
- Klein finds that his second-order iterative algorithm is more accurate than Kahan to compute the sum. I find the same accuracy as Kahan (close to 32-bit machine epsilon).
- When the set of random numbers is ordered, the second order iterative algorithm is significantly worse than Kahan. Kahan keeps the same accuracy as on the ordered set.
- Using longer or shorter sequences or different random number sequences lead to the same observations.
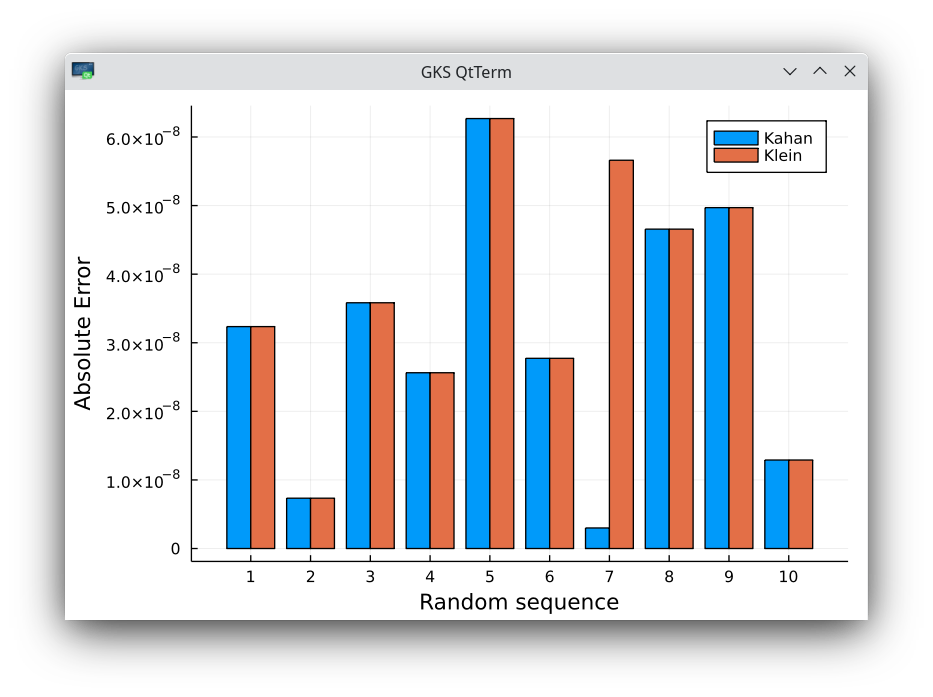
Absolute errors on 10 random sequences of 50 million numbers in 32-bit arithmetic. The 7-th sequence shows a small difference in favor of Kahan.
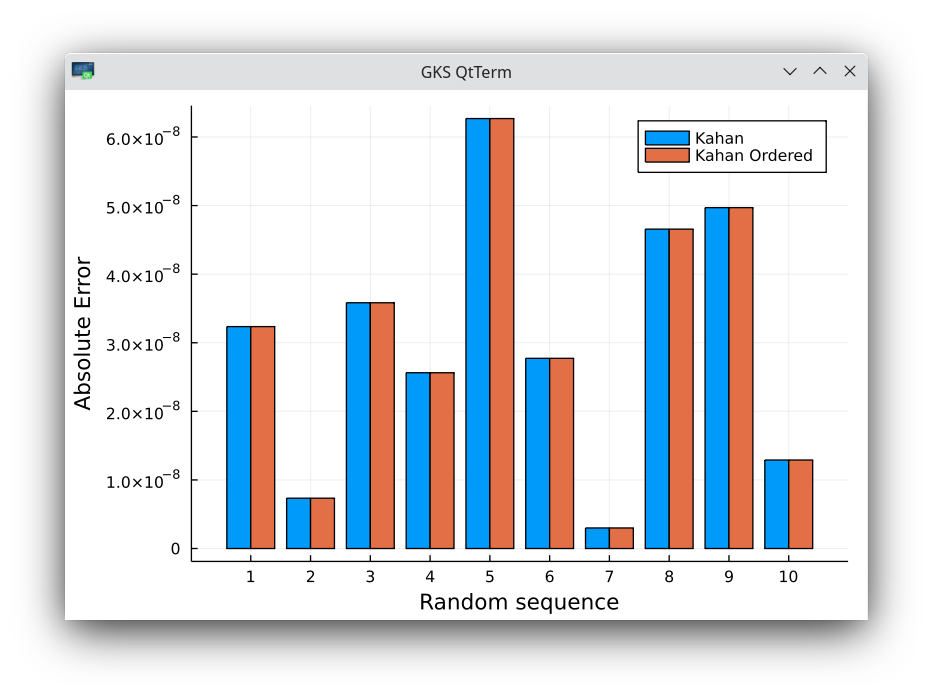
Absolute errors on 10 random sequences of 50 million numbers in 32-bit arithmetic, comparing with the same set of numbers, used in ascending order for the algorithm of Kahan. No difference at all.
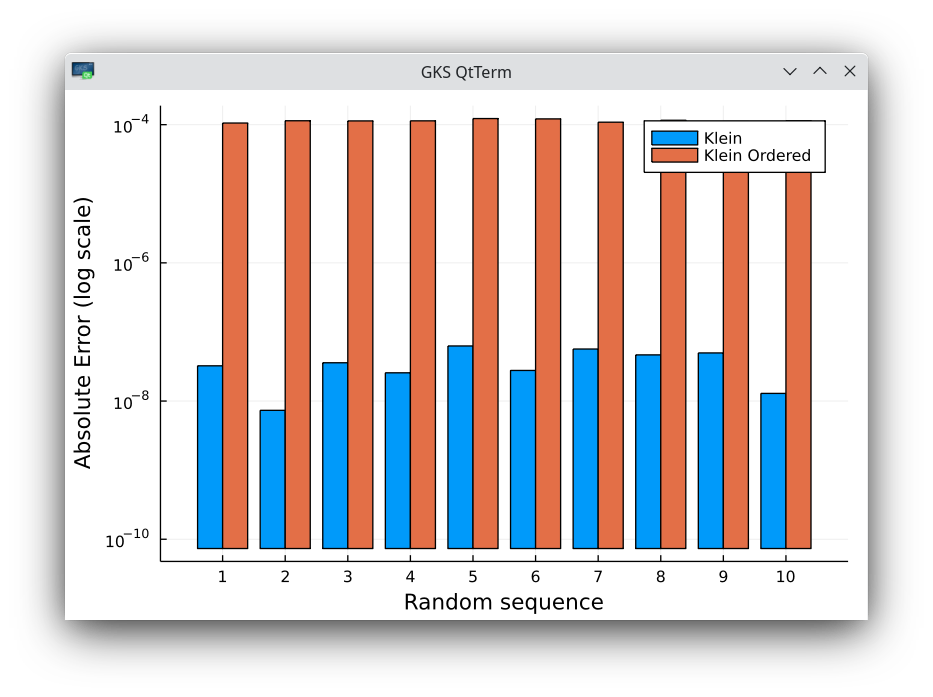
Absolute errors on 10 random sequences of 50 million numbers in 32-bit arithmetic, comparing with the same set of numbers, used in ascending order for the algorithm of Klein. Note the log scale and large error differences.
I attempted to contact the author (who also works on cryptography) alas with no success (the various e-mail addresses are not valid anymore). I contacted two different developers who implemented the algorithm from Klein in their own libraries. Their feedback is interesting:
- Both did not try to reproduce the results of the paper. On one hand, this is slightly surprising, since the test seems so simple to try out. On the other hand, results of published papers are unfortunately rarely being reproduced, especially by referees.
- Both implemented a version hardcoded for 64-bit floating point numbers.
- One of the developers implemented this also in the context of parallel Monte-Carlo simulations. So it is a well known practical problem.
- One of the developers suggested Kahan was indeed as good on his problems.
I wrote a note based on my experiments, and with more details on:
- the kinds of Monte-Carlo simulations in finance,
- reproducible greeks,
- concrete examples
The note in on arxiv, with code on github.