Efficient Finite Difference Grid Stretching for Finance
Discontinuities in the payoff or its derivatives are common in financial PDEs. If not handled properly, those discontinuities may decrease the accuracy of the finite difference scheme significantly. Are insertions at relevant locations good enough? What about streched grids? A new efficient stretching is proposed.
August 28, 2022
Partial differential equations sometimes have critical points where the solution or some of its derivatives are discontinuous. The simplest example is a discontinuity in the initial condition. It is well known that those decrease the accuracy of finite difference methods. A common remedy is to stretch the grid, such that many more grid points are present near the critical points, and fewer where the solution is deemed smooth. An alternative solution is to insert points such that the discontinuities fall in the middle of two grid points.
This situation arises in the pricing of nearly all financial derivative contracts. The vanilla European option of given maturity and strike price, the simplest non-linear contract, has indeed a discontinuous first derivative at the strike price. Barriers with a discrete monitoring schedule are also a very common feature in more exotic contracts. Those create a discontinuity at the barrier level.
Tavella and Randall propose two solutions to improve the convergence somewhat significantly:
- A smooth deformation to place the critical points typically in the middle of two grid points (alternatively, at some specific grid points).
- An hyperbolic stretching to concentrate points near the critical point(s).
Inserting points at given locations is a possible simple alternative. Clearly, the non-smoothness may be problematic for a clear theoretical order of convergence. But does it improve the accuracy towards a raw uniform or stretched grid? Is a smooth deformation always preferable?
I explore those questions in a new paper Inserting or Stretching Points in Finite Difference Discretizations. It is found that the approach of Tavella and Randall allow to increase the accuracy reliably and significantly, using concrete examples in finance, while insertion may still be an interesting straightforward alternative to apply on top of a stretched grid.
There is however a practical issue with Tavella and Randall: the stretching is slow, and cumbersome to implement for multiple critical points. Indeed, it involves solving numerically an ODE. The ODE is typically discretized with a fourth-order Runge-Kutta scheme, but the solver may be more challenging to make robust. Is there another kind of stretching with similar properties but that is much faster and simpler to code? The paper details a new piecewise-cubic stretching with those properties.
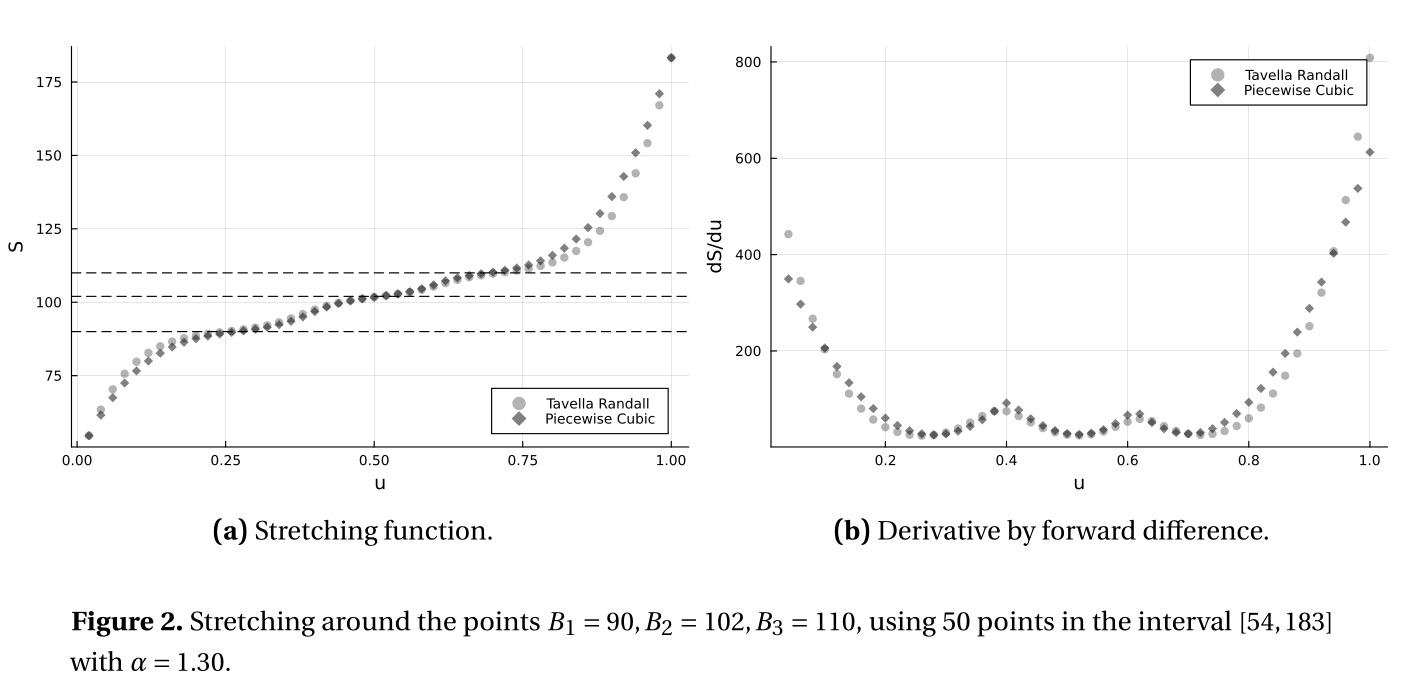
The below figure presents how the grid transformation “looks” compared to the Tavella-Randall approach:
In terms of accuracy, the following table summarizes the error (x10000) in the price of the same knock-out barrier option of maturity T=1 year, strike K=150 and barrier B=125, with 250 discrete observations dates, starting at $$t_1=1/250$$ until $$t_{250}=T=1$$ under the Black-Scholes model with dividend yield q=0.02, interest rate r=0.07 and volatility \sigma=20%, presented in Tables 6.1 and 6.2 of Tavella and Randall book. The main difference with the paper and the book is that below, I use two critical points, one at the strike, one at the barrier level, while the paper and the book use only one critical point at the barrier level.
| Grid type | Grid size | Uniform | Cubic | Tavella-Randall | |
|---|---|---|---|---|---|
| Raw | 250 | 5002 | 735 | 783 | |
| 500 | 74 | 173 | 324 | ||
| 1000 | 1084 | 113 | 90 | ||
| 2000 | 61 | 36 | 32 | ||
| Insertion | 250 | 320 | 79 | 77 | |
| 500 | 143 | 17 | 19 | ||
| 1000 | 29 | 4 | 4 | ||
| 2000 | 8 | 1 | 1 | ||
| Deformation | 250 | 633 | 45 | 51 | |
| 500 | 153 | 11 | 13 | ||
| 1000 | 38 | 3 | 3 | ||
| 2000 | 9 | 0.7 | 0.7 |
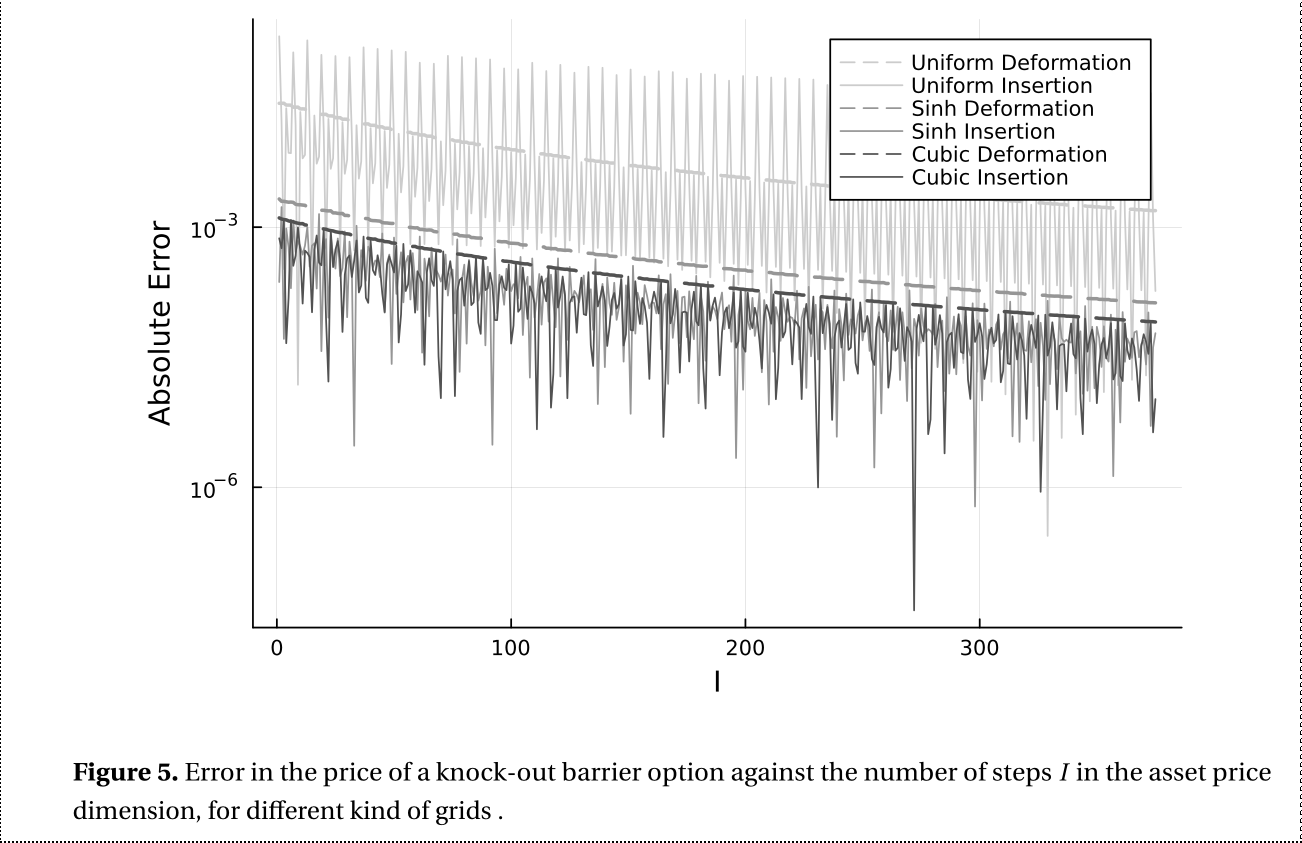
Insertion looks good, but this is highly dependent on the grid size, here is an excerpt from a relevant Figure from the paper that illustrates this point:
The paper on arxiv.