A spline to fill the gaps with Andreasen-Huge one-step method
I recently stumbled upon a blog which suggested to not stay flat with Andreasen-Huge arbitrage free volatility interpolation method. What about using a spline?
May 11, 2017
I recently stumbled upon a blog which suggested to not stay flat with Andreasen-Huge arbitrage free volatility interpolation method. The paper from Andreasen and Huge specifies a piecewise constant (single-step) local volatility where the number of constants matches the number of market option prices.
The blog post shows eventual unstability with the piecewise constant approach, not visible with a linear interpolation. I wondered then if we should not go to the next level: use a spline on N values where N is the number of market options prices. Using a spline to represent the local volatility is a very common idea, for example it is in the large-step local volatility method of Reghai-Boya-Vong.
I tried this idea on SPX500 options of maturity 1 year and stumbled upon erratic behavior depending on the number of nodes used in the grid. In reality, this was due to using the wrong monotone interpolation. I had used Hyman-Dougherty monotone interpolation by habit. But the data is far from being monotone, and the Hyman interpolation does not necessarily behave well on non-monotone data: by design, it can still wiggle over or under the nodes. This is what happens on the figure below, which zooms problematic region of the local variance: it becomes negative with Hyman interpolation.
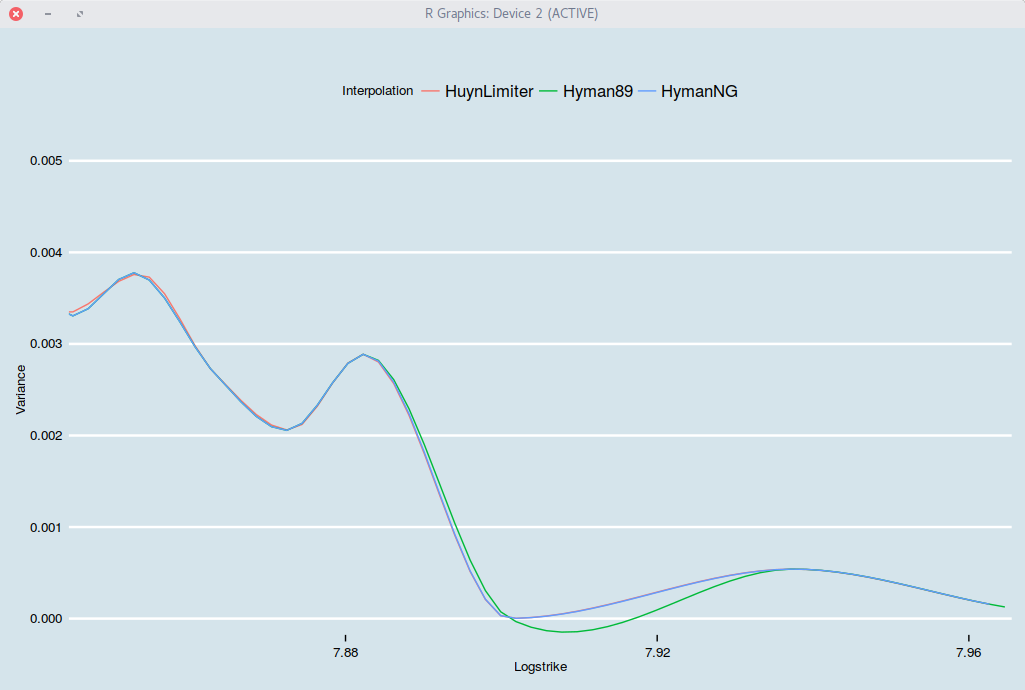
Local variance as a function of the log-strike. Zoom on the problematic region with Hyman interpolation.
A real monotone interpolation, without the problems of the discontinuity introduced by the Hyman approach as evidenced in the paper Stable Interpolation for the Yield Curve, but not well-known, is the rational limiter of Huynh. It is also possible to simply use the non-negative interpolation of Hyman-Dougherty (denoted as Hyman-NG in the figure), but in theory, this will introduce a discontinuity, which could be problematic in the optimization routine.
It works well with a properly monotone spline, but how does the one-step local volatility looks like?
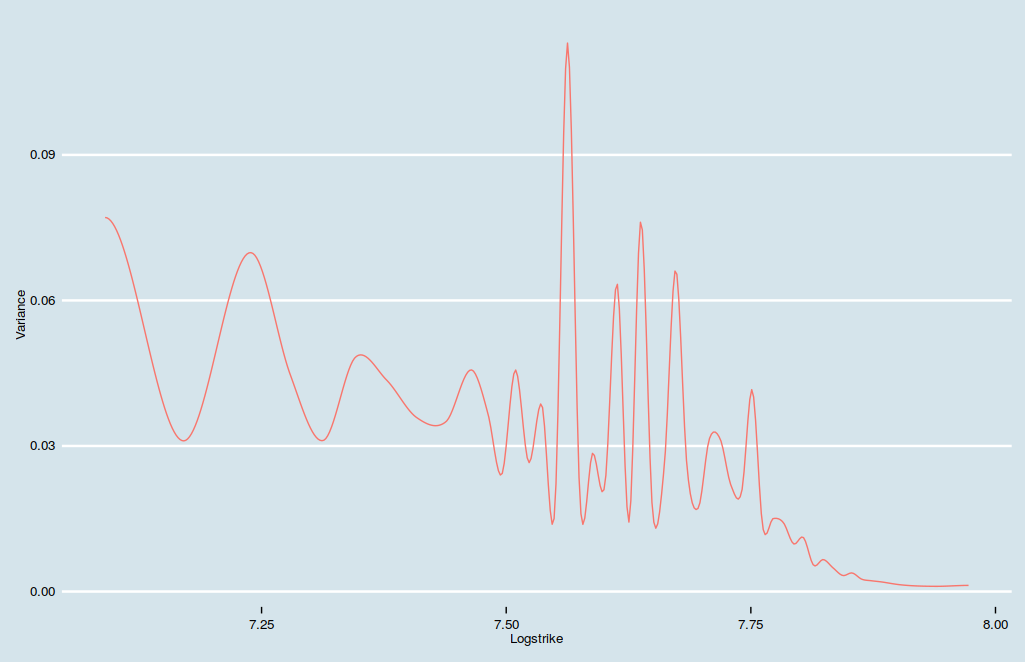
Local variance as a function of the log-strike with Huynh rational limiter.
With so many wiggles in the local volatility, it is not obvious this is really preferable to a linear interpolation.